x趋于0时的等价替换及其适用条件

等价无穷小的定义：
若，则与是等价无穷小的，记作 . 即当两个函数相比取极限，如果极限值为1，则这两个函数是等价无穷小的。

常用的等价替换（x趋于0时）

==等价替换的本质是当x趋于某一点时，两个函数在该点处相切，即两函数在该点处斜率相同且只有该点处一个交点。== 斜率相同，意味着两函数在该点处具有相同的增长率，在x的值无尽逼近于该点时，两函数值几乎相同，所以在求极限的时候可以用等价替换，来简化问题。从斜率（函数变化率）的角度也更容易理解洛必达法则。

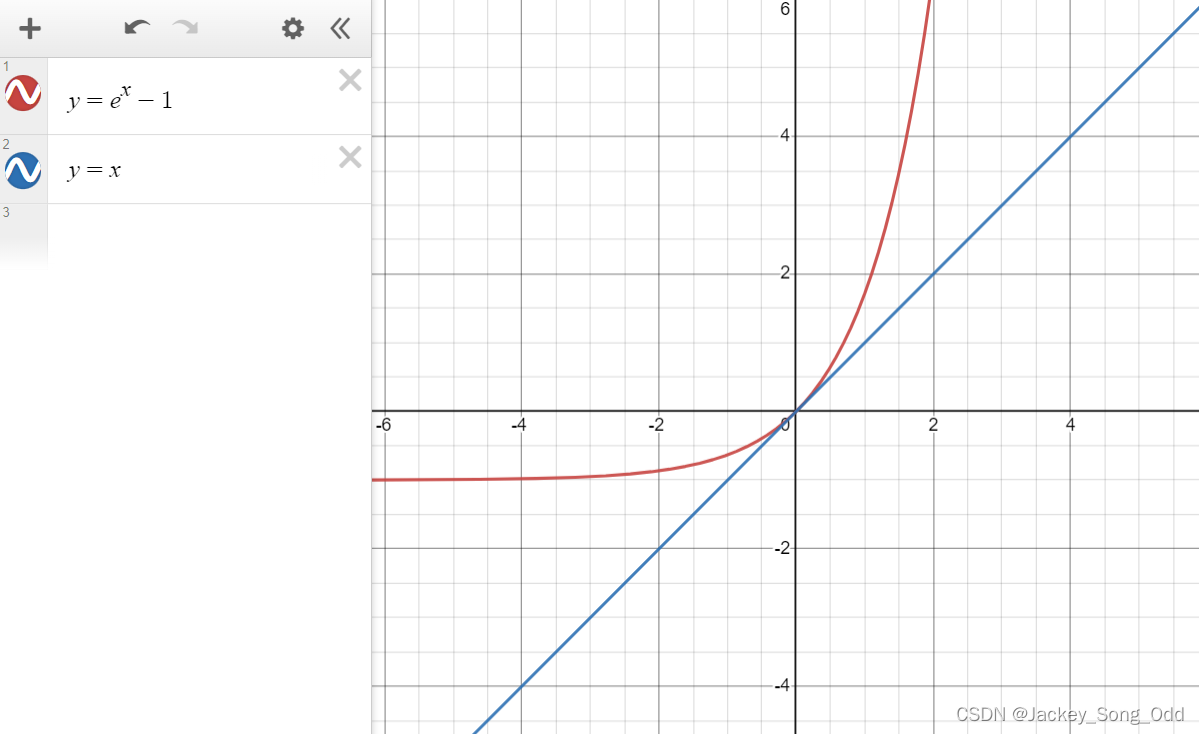
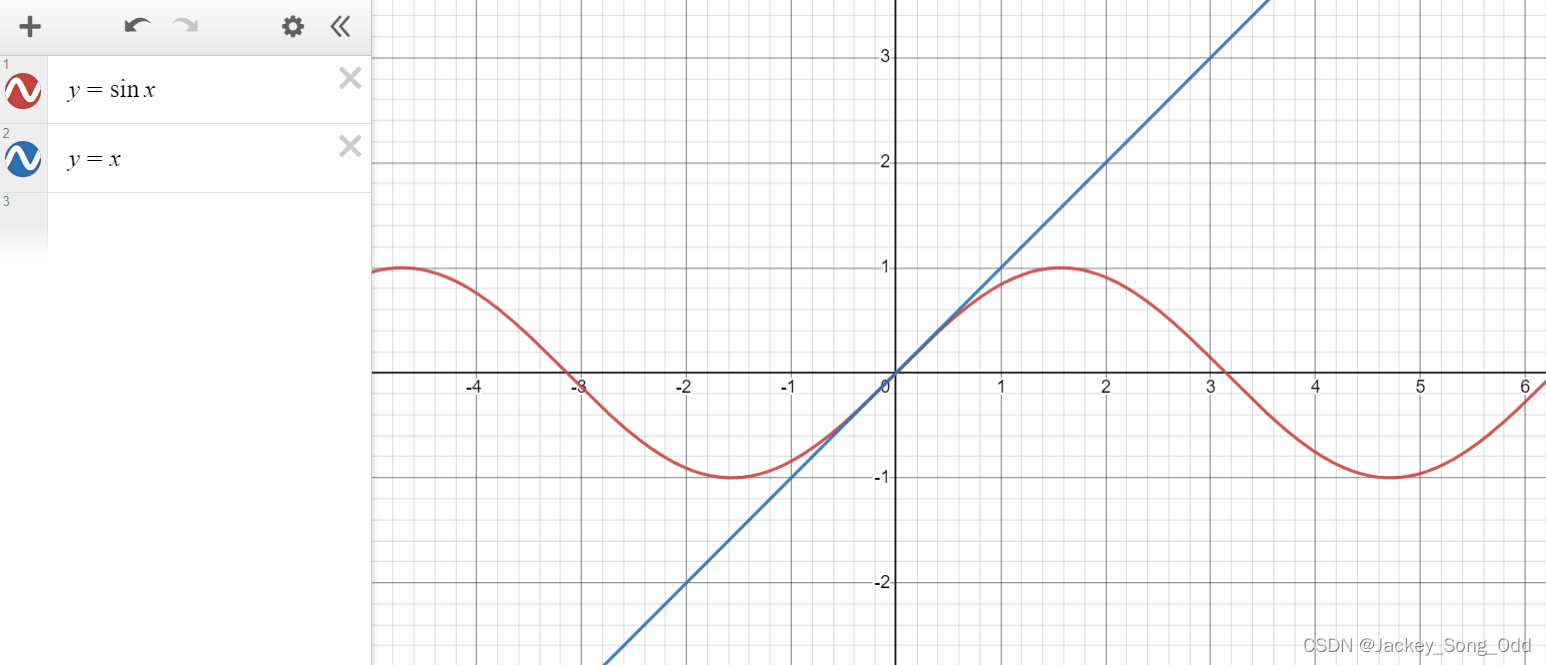
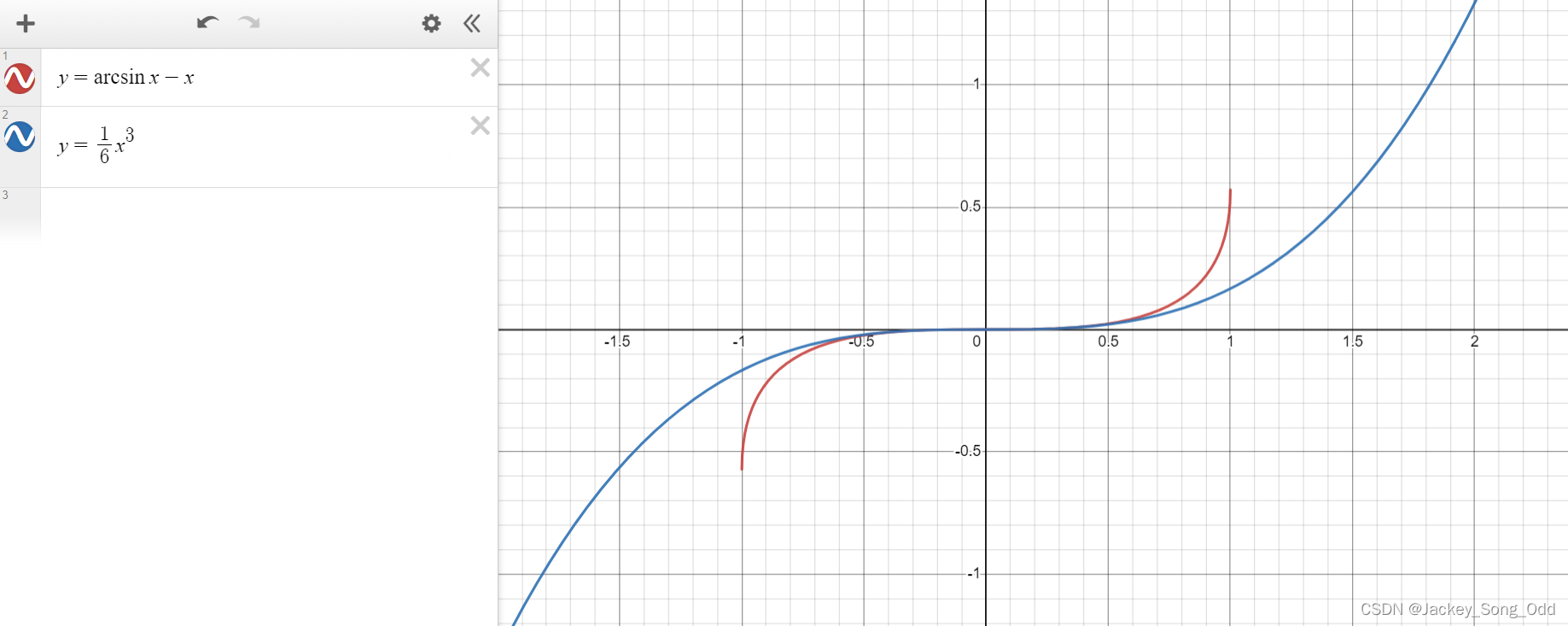
洛必达法则：设
(1) 当时，函数及都趋于 0；
(2) 在点的某去心领域内，及都存在且；

(3) 存在（或为）

则 .

洛必达法则使用于以下类型的极限中：(未定式类型)

在求极限问题中，不是所有的情况都是可以直接用等价替换的。

从等价无穷小的定义中可以看出，与的极限比值为1，所以在乘除关系中，可以使用等价无穷小进行替换。

等价替换适用于乘除关系中，部分加减关系中可以用等价无穷小替换。大致如下：

简单地讲就是，若极限的分子分母中有加减关系，且等价替换后加减关系的结果为0，这时候一般不能用等价替换。