---

---

---

牛顿迭代法（Newton’s Method）又称 牛顿-拉夫森方法（Newton-Raphson Method），是一种用于求解实数或复数函数零点（根）的数值分析方法。该方法通过不断迭代逼近方程的解，通常收敛非常迅速，特别是当初始猜测值接近真实解时。

牛顿迭代法的基本思想是利用函数的泰勒展开式的线性近似来不断逼近零点。

假设有一个函数 ，要找到 的 值。

如果 是当前的近似值，那么牛顿迭代法给出的下一步近似值 则可以通过以下公式计算：

其中， 是 函数 在 处的值。
是 函数 在 处的导数值。

---

几何意义： 点做切线，与 轴的交点则为下一个近似值 。

， 假设 ，做切线：

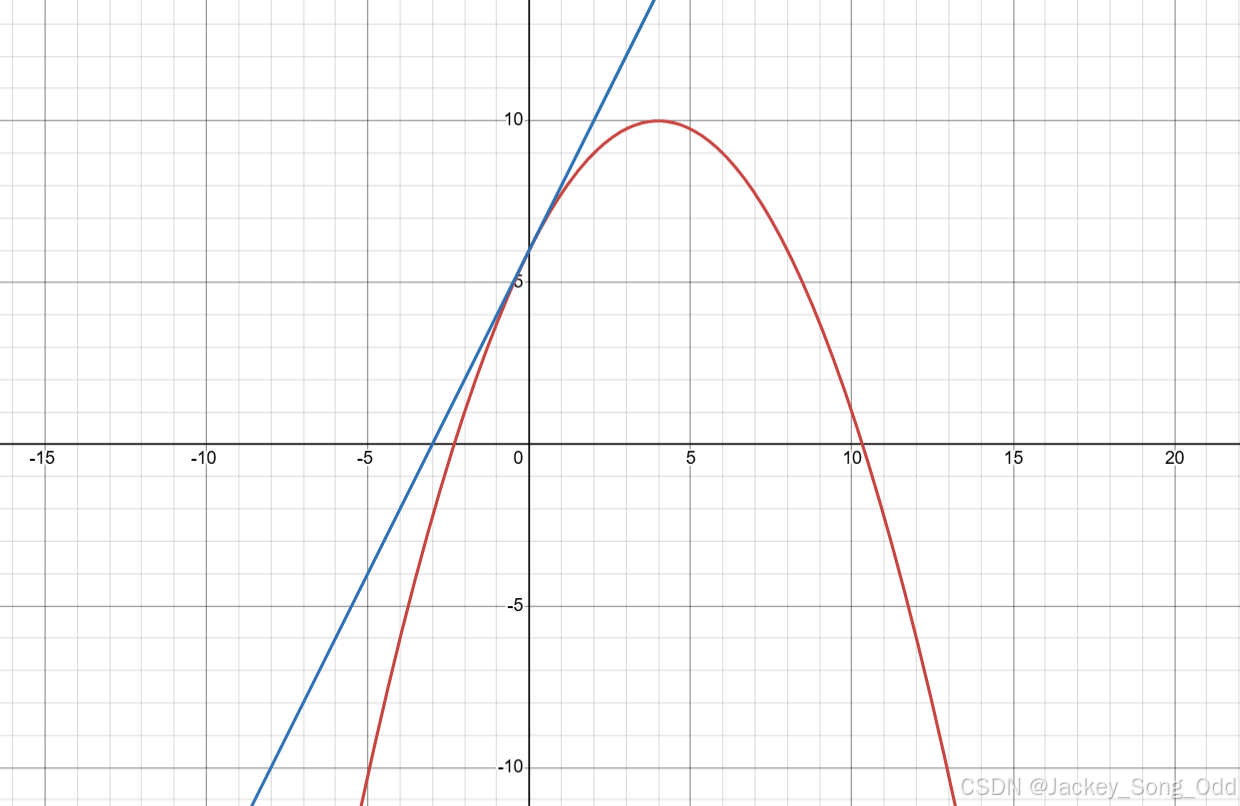
与 轴交点 ， 。

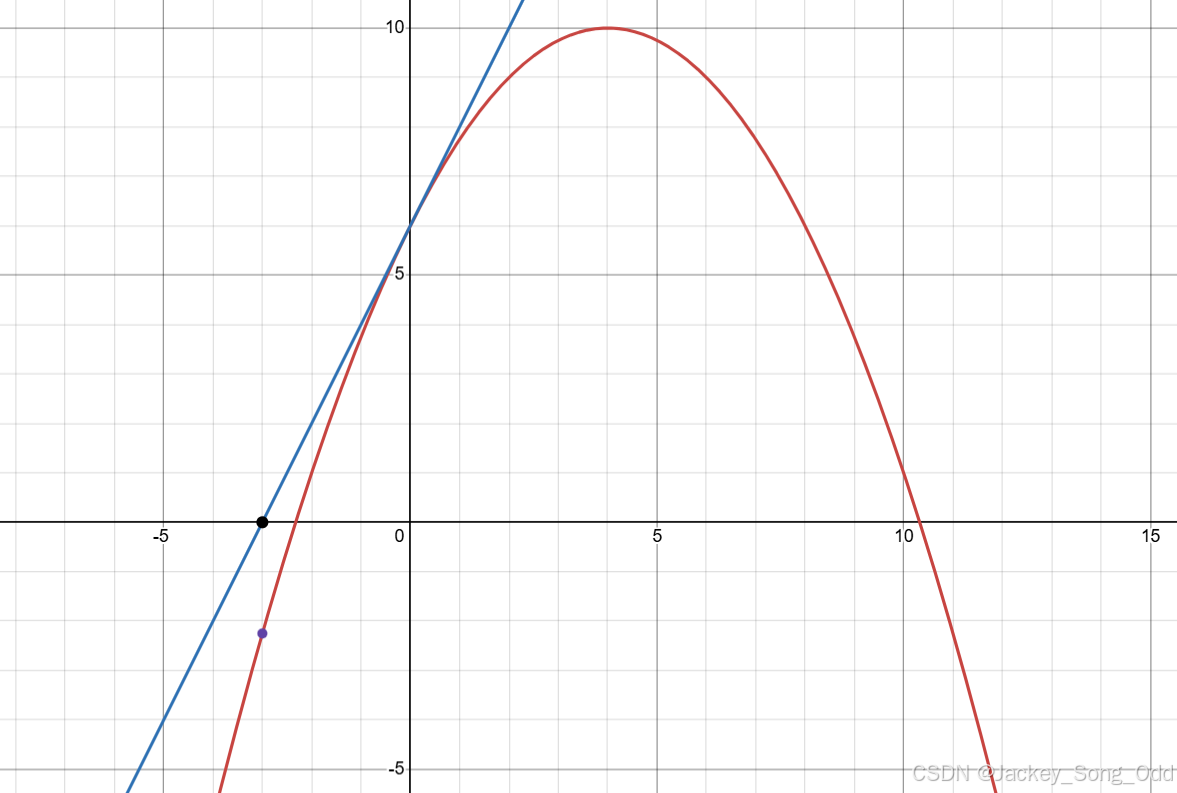
点做切线：

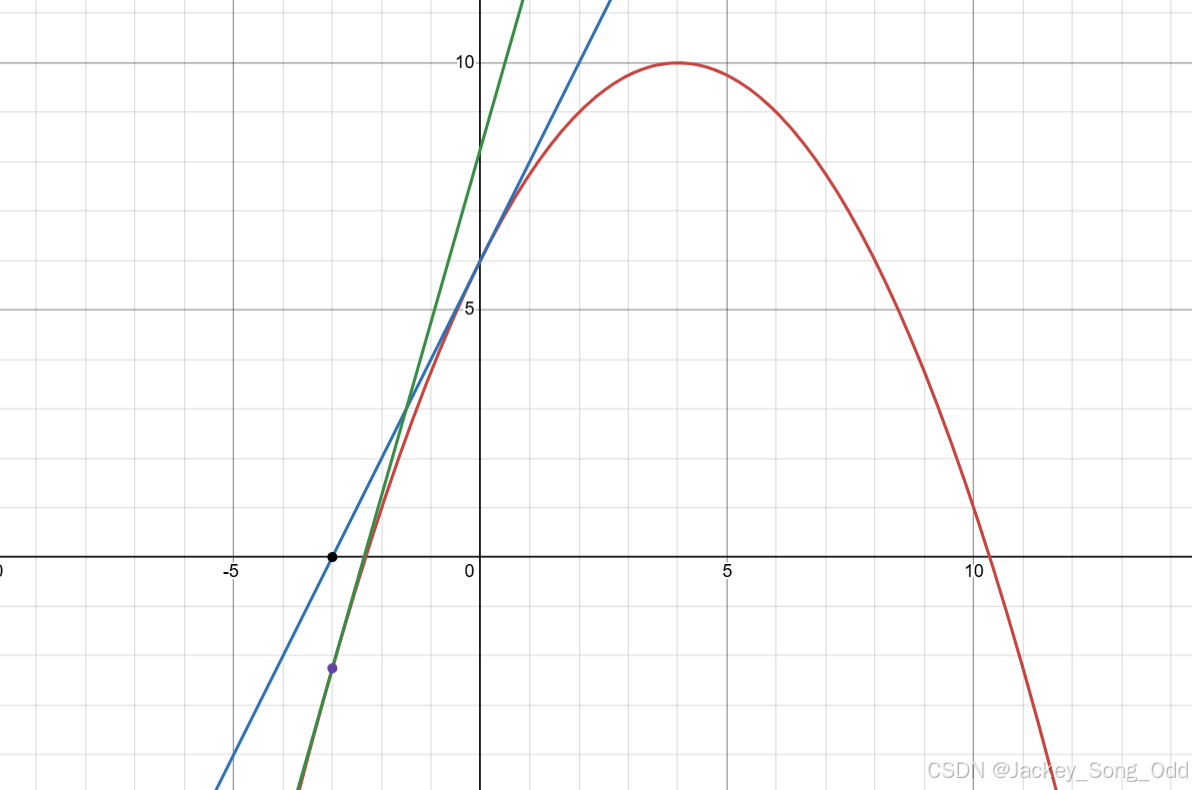
不断迭代，切线与 轴交点无线逼近零点。

---

切线斜率 .

---

C语言计算立方根算法，不使用库函数，牛顿迭代法实现，保留小数点后一位。

的解。

double x_next = (2 * x + a / (x * x)) / 3.0;

#include <stdio.h>

// 牛顿迭代法计算立方根
double cube_root(double a) {
    if (a == 0) {
        return 0;  // 如果 a 为 0，立方根是 0
    }

    double x = a / 3.0;  // 初始猜测
    double epsilon = 0.0001;  // 精度阈值
    double difference;

    // 不断迭代直到结果足够精确
    do {
        double x_next = (2 * x + a / (x * x)) / 3.0;
        difference = (x_next > x) ? (x_next - x) : (x - x_next);  // 计算误差
        x = x_next;
    } while (difference > epsilon);

    return x;
}

int main() {
    double a;
    scanf("%lf", &a);
    printf("%.1f", cube_root(a));
    return 0;
}

不使用库函数，计算 算术平方根：

#include <stdio.h>

// 牛顿迭代法计算平方根
double square_root(double a) {
    if (a < 0) {
        printf("负数没有实数平方根\n");
        return -1;  // 返回 -1 表示错误，负数没有实数平方根
    }
    if (a == 0) {
    	return 0;
	} 

    double x = a / 2.0;  // 初始猜测值
    double epsilon = 0.000001;  // 精度阈值
    double difference;

    // 不断迭代直到结果足够精确
    do {
        double x_next = (x + a / x) / 2.0;  // 牛顿迭代公式
        difference = (x_next > x) ? (x_next - x) : (x - x_next);  // 计算误差
        x = x_next;  // 更新 x 为新的估计值
    } while (difference > epsilon);  // 如果误差大于 epsilon，继续迭代

    return x;  // 返回最终的平方根估计值
}

int main() {
    double number;
    scanf("%lf", &number);

    double result = square_root(number);
    
    if (result != -1) {
        // 输出结果，保留一位小数
        printf("平方根是：%.1f\n", result);
    }

    return 0;
}