---

---

---

如果你经常刷一些算法题，那么你一定经常遇到动态规划这一类问题。

那么是什么是动态规划呢？

Dynamic programming is a computer programming technique where an algorithmic problem is first broken down into sub-problems, the results are saved, and then the sub-problems are optimized to find the overall solution — which usually has to do with finding the maximum and minimum range of the algorithmic query. （动态规划 (Dynamic Programming 简称 DP) 是一种计算机编程技术，首先将算法问题分解为子问题，保存结果，然后优化子问题以找到整体解决方案，这通常与找到算法查询的最大和最小范围有关。）

以上便是一个动态规划的解释，读起来很抽象，实际上很简单。我们先来看一个动态规划的经典例子 —— 小孩爬楼梯问题。

问题：一个小孩去爬楼梯，一步只能爬 1 阶或 2 阶楼梯，那么爬上总共有 n 阶的楼梯共有多少种方法？

乍一看到这问题，可能会束手无策。不过我们可以简单地来分析一下：

• 假设 n = 7，我们可以把问题分解：
  • 由于小孩一步只能爬 1 阶或者 2 阶，所以想要爬上第 7 阶楼梯，小孩可以从第 5 阶爬 2 阶或者从第 6 阶爬 1 阶到达第 7 阶。
  • 而想要爬到第 6 阶，可以从第 4 阶爬 2 阶，或者从第 5 阶爬 1 阶。
  • … …

我们可以定义一个函数 f(n) 表示爬上第 n 阶楼梯共有多少种方法。所以我们就可以得到以下递推公式：

f(n) = f(n - 1) + f(n - 2) 。

n = 7 时就有：

• f(7) = f(6) + f(5)
• f(6) = f(5) + f(4)
• … …
• f(3) = f(2) + f(1)
• 当 n 等于 2 时，小孩可以分两步，每步跨一阶上去，也可以直接一步跨两阶上去，所以有两种跨法， f(2) = 2 。
• 很显然，f(1) = 1 。

我们可以先使用函数的递归调用来解决这个问题：（C语言代码）

#include <stdio.h>
int climbStairs(int n) {
    if (n == 1)
        return 1;
    if (n == 2)
        return 2;
    return climbStairs(n - 1) + climbStairs(n - 2);
}
int main(void) {
    int n;
    scanf("%d", &n);
    printf("%d", climbStairs(n));
    return 0;
}

n = 1，和 n = 2 就是临界条件，如果 n 既不等于 1 也不等 2，那么函数 climbStairs() 就调用它自己，分别计算 n - 1 和 n - 2 的值，相加再返回。在这个过程种，函数 climbStairs() 不断调用自己，就叫做函数的递归调用。climbStairs() 在递归调用的过程中，会产生很多分支，构成一个树，用图形来表示如下：

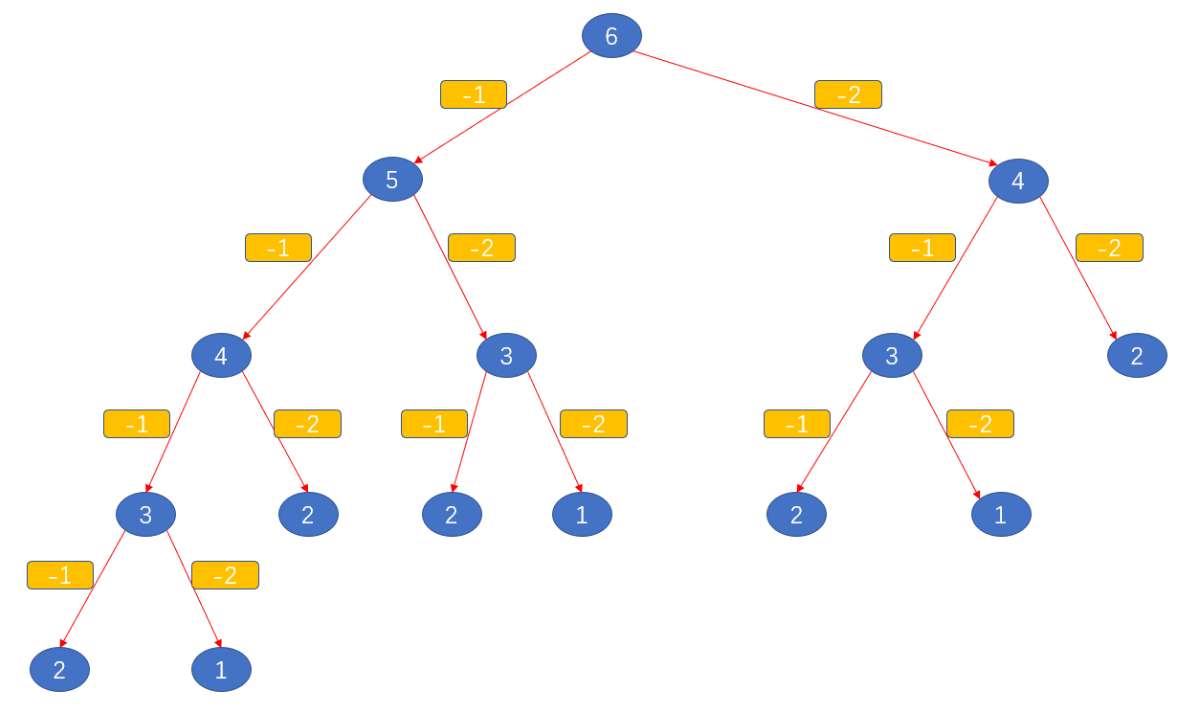
从树状图中我们就可以看到，使用递归调用产生了大量的重复计算，例如 n = 4 时被计算了两次，n = 3 被计算了 3 次。当 n 的值非常大时，这样的重复计算会非常多。由于递归树的节点数是指数级增长的，重复计算了许多子问题，因此时间复杂度是 O(2^n)。递归调用栈是每次递归调用时保存的函数调用信息，包括函数参数、局部变量和返回地址。空间复杂度主要由递归的最大深度决定。因此以上算法的空间复杂度是 O(n)。

为了优化以上算法，我们可以在调用的过程中保存每次计算的结果。每次进行递归调用时，从保存的结果中查询，如果已经存在就不用再递归了，直接使用。所以 动态规划 可以看成是一个有记忆的递归算法。

优化后的 C语言代码：

#include <stdio.h>
int climbStairsHelper(int n, int* memo) {
    if (n == 1) return 1;  // 1 阶有 1 种方法
    if (n == 2) return 2;  // 2 阶有 2 种方法
    // 如果已经计算过这个子问题，直接返回结果
    if (memo[n] != -1) return memo[n];
    // 计算并保存结果
    memo[n] = climbStairsHelper(n - 1, memo) + climbStairsHelper(n - 2, memo);
    return memo[n];
}
int climbStairs(int n) {
    // 创建一个数组来保存子问题的结果
    int memo[n + 1];
    // 初始化 memo 数组为 -1，表示尚未计算
    for (int i = 0; i <= n; i++) {
        memo[i] = -1;
    }
    return climbStairsHelper(n, memo);
}
int main(void) {
    int n;
    scanf("%d", &n);
    printf("%d", climbStairs(n));
    return 0;
}

使用了 “带有备忘录的递归调用”，树状图中就不会有那么多的分支了，所以就构成了一个有向无环图。

例如 n = 10，有向无环图：

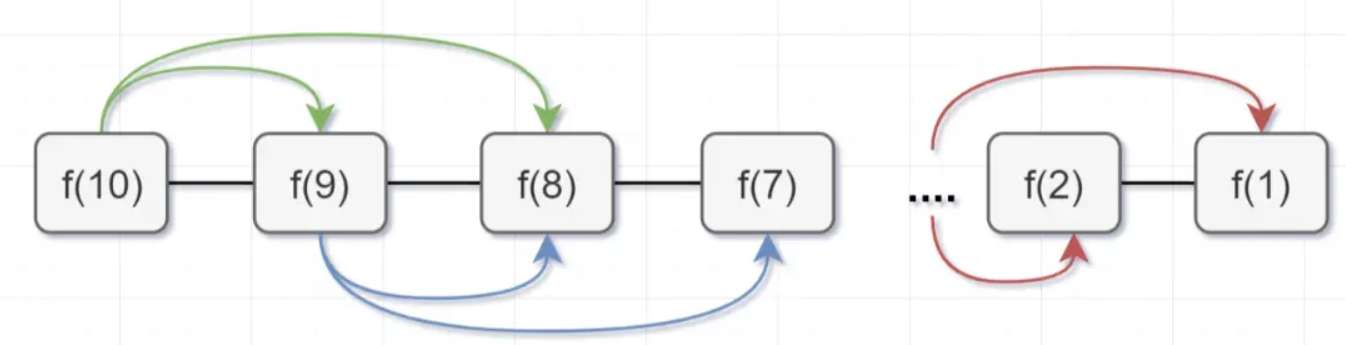
因此，我们可以用有向无环图来很方便地描述动态规划问题。

以上解决小孩爬楼梯的代码都是从顶端往下推，也可以从下网上推（斐波那契数列）。

• 初始化两个值：f(-1)=0, f(0)=1。则 f(n)=f(n-2) + f(n-1)，n 大于等于1。

代码如下：

#include <stdio.h>
int climbStairs(int n) {
	int a = 0, b = 1, sum = 0; 
	for (int i = 0; i < n; i++) {
		sum = a + b;
		a = b;
		b = sum;
	}
	return sum;
} 
int main() {
	int n;
	scanf("%d", &n);
	printf("%d", climbStairs(n));
	return 0;
}

---

---

---

简单总结：动态规划是一种用于解决具有最优子结构和重叠子问题性质的复杂问题的算法技术。它将问题分解为子问题，通过保存子问题的解来避免重复计算，最终得到原问题的解。动态规划通常用来求解最优化问题，例如最短路径、最大收益等。

动态规划的核心思想：

• 最优子结构：问题的最优解可以通过子问题的最优解来构造。
• 重叠子问题：原问题可以被分解为若干个子问题，并且这些子问题会被多次计算。

动态规划的步骤：

• 定义状态：确定如何表示子问题的解，通常通过数组或矩阵来表示状态。
• 状态转移方程：确定如何通过已知的子问题解来构建当前问题的解。即建立一个递推关系。
• 初始化边界条件：确定最小的子问题的解，也就是基础情况。
• 填充表格：根据状态转移方程，从小问题开始逐步求解大问题，最终得到原问题的解。

动态规划的两种常见实现方式：

• 自顶向下（递归 + 记忆化搜索）：采用递归的方式解决问题，同时使用一个数据结构（如数组、哈希表等）保存已经计算过的子问题解，避免重复计算。
• 自底向上（迭代）：从最简单的子问题开始逐步解决，直到解决原问题。通过填充一个表格，逐步得到答案。

经典的动态规划问题：

• 背包问题：给定一组物品和背包的容量，选择物品放入背包，使得背包中物品的总价值最大化。
• 最长公共子序列：给定两个字符串，求它们的最长公共子序列。
• 最短路径问题：在一个加权图中，求从一个节点到另一个节点的最短路径。
• 等等… …

---

---

---