最长无重复字符子字符串问题（Longest Substring Without Repeating Characters）
Published in：2024-12-19 |

问题描述

原题：

Longest Substring Without Repeating Characters

Given a string s, find the length of the longest substring without repeating characters.

Example 1:

1
2
3
Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.

Example 2:

1
2
3
Input: s = "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

Example 3:

1
2
3
4
Input: s = "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.

Constraints:

  • 0 <= s.length <= 5 * 104
  • s consists of English letters, digits, symbols and spaces.

翻译：

最长无重复字符子字符串

给定一个字符串 s，找到长度最长的没有重复字符的子字符串。

例1：

1
2
3
输入: s = "abcabcbb"
输出: 3
解释: 答案是 "abc", 长度为 3.

例2：

1
2
3
输入: s = "bbbbb"
输出: 1
解释: 答案是 "b", 长度为 1.

例3：

1
2
3
4
输入: s = "pwwkew"
输出: 3
解释: 答案是 "wke", 长度为 3.
注意答案必须是一个子字符串, "pwke" 是一个子序列但不是一个子字符串.

限制：

  • 0 <= s.length <= 5 * 104
  • s 由英文字母、数字、符号和空格组成。

Solution 1：解决方案一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int insubstr( char* s, char ch, int c) {
	for (int i = 0; i < c; i++)
		if (ch == *(s + i))
			return 1;
	return 0;
}

int lengthOfLongestSubstring(char* s) {
	int c = 0;
	char sub[50001] = { 0 };
	char maxSub[50001] = { 0 };
	int i;
	for ( i = 0; *(s + i) != 0; i++) {
		if (!insubstr(sub, *(s + i), c)) {
			sub[c++] = *(s + i);
		} else {
			sub[c] = 0;
			if (strlen(sub) > strlen(maxSub))
				strcpy(maxSub, sub);
			i = i - c;
			sub[0] = 0;
			c = 0;
		}
	}
	if ( strlen(sub) == strlen(s) ) {
		return strlen(sub);
	}
	else if ( strlen(sub) > strlen(maxSub)){
		return strlen(sub);
	} else {
		return strlen(maxSub);
	}
}

提交代码：过辣！！！从下图中可以看到，运行时间为 191ms，打败了 8.99% 的人。为什么 191ms 这么大？因为本题的测试用例的数据量可能非常大，内存使用是 8.81 MB，同样也是测试用例数据量太大造成的。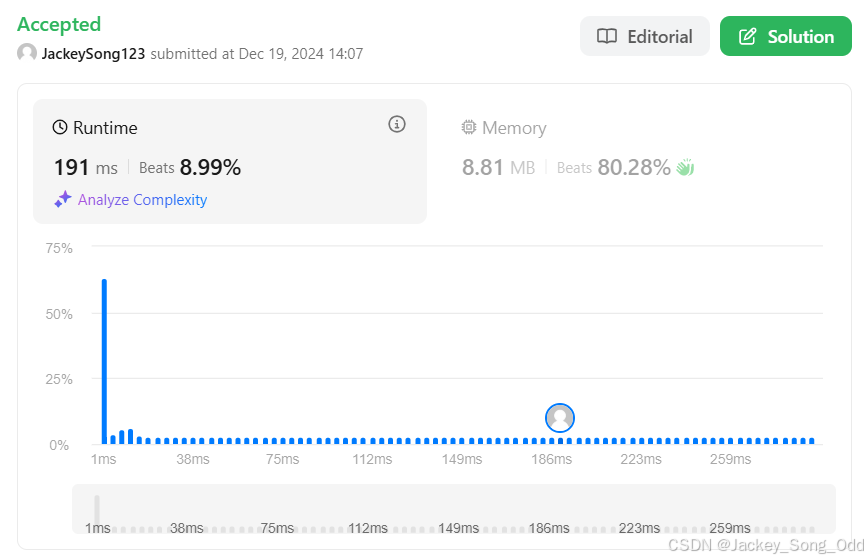
在这里插入图片描述

Solution1 解释：

自己写的代码，没有写注释几天后就看不懂了，还要重新理解。所以，温馨提示，写代码最好还是写了注释，否则，无论你记忆多好，时间久了都会忘记当时的思路。

int insubstr( char* s, char ch, int c); 该函数接收一个字符串指针，一个字符，和字符串的长度，判断字符 ch 是否在字符串 s 中，如果在返回1，不在返回0。

在 int lengthOfLongestSubstring(char* s) 函数体中，sub 用来保存临时的子字符串，maxSub 用来保存最大的无重复字符的子字符串。变量 c 作为 sub 的下标。从下标零开始遍历传入的字符串 s ，如果当前字符不在 sub 中，则将当前字符保存至 sub 数组中，如果当前字符在 sub 中，则出现了重复字符。

如果出现了重复字符，则和 maxSub 进行比较，如果长度大于 maxSub ，则将当前 sub 中的字符串复制到 maxSub 中。然后 i 从 i - c 处开始，重置 sub[0]=0;、c=0;，继续寻找没有重复字符的子字符串，然后重复上面的步骤。

循环结束后，如果 sub 的长度就等于 s 的长度，说明没有任何重复字符。直接返回 strlen(sub); 。还有一种情况，无重复子字符串在整个 s 的最后面，for 循环结束了，没有比较 sub 和 maxSub 的长短，则在 for 循环结束后，进行比较，并返回长的那一个。不是以上两种情况，直接返回 strlen(maxSub) 的值。

Solution1 时间复杂度分析：

  1. 外层循环：在 lengthOfLongestSubstring 函数中，外层 for 循环遍历了整个字符串 s。假设字符串的长度为 n，该循环会执行 n 次。因此，外层循环的时间复杂度是 **O(n)**。

  2. **内层调用 insubstr**：每次外层循环内调用 insubstr 函数，来检查字符是否已经在当前的子串 sub 中。insubstr 函数的时间复杂度是 **O(c)**，其中 c 是当前子串的长度。最坏情况下，c 可能会达到 n（即当字符串中没有重复字符时），因此 insubstr 最坏的时间复杂度是 **O(n)**。

  3. 内层的 insubstr 被调用 n 次：在最坏情况下，insubstr 会被外层循环调用 n 次，每次调用的时间复杂度是 O(n)。因此，总的时间复杂度是 **O(n^2)**。

  4. strlen(sub) 和 strlen(maxSub) 的调用：在代码中，strlen(sub) 和 strlen(maxSub) 也被调用了多次。由于每次调用 strlen 都需要遍历字符串来计算长度，因此每次调用 strlen 的时间复杂度是 **O(c)**，其中 c 是子串的长度，最坏情况下为 **O(n)**。但这在每次 insubstr 调用时都会发生，因此整体的时间复杂度增加。

    由于每次 strlen 最坏情况下都会遍历整个子串，最坏情况是 **O(n)**，因此 strlen(sub) 和 strlen(maxSub) 的时间复杂度加起来是 **O(n)**。因此这些调用的总时间复杂度仍然是 **O(n^2)**。

Solution1 总体的时间复杂度为 **O(n^2)**。这是因为在最坏的情况下，insubstr 和 strlen 都会触发 O(n) 的操作，而这种操作会在外层的每次循环中发生。

Solution1 空间复杂度分析：

  1. **子串数组 sub 和 maxSub**：这两个数组的最大大小是 50001，分别存储当前的子串和最长的子串，因此这两个数组的空间复杂度是 **O(n)**，其中 n 是字符串的长度。
  2. 辅助变量：除了 sub 和 maxSub 外，程序还使用了几个辅助变量（如 i, c 等），这些变量占用的空间是常数级别的 **O(1)**。

由于 sub 和 maxSub 是固定大小的数组，因此空间复杂度主要来自这两个数组。整体的空间复杂度为 **O(n)**。

Solution2：解决方案2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int lengthOfLongestSubstring(char* s) {
    int map[128] = { 0 };
    int left = 0, right = 0, maxLength = 0;
    int n = strlen(s);
    while (right < n) {
        if (map[s[right]] > 0) {
            left = (map[s[right]] > left) ? map[s[right]] : left;
        }
        map[s[right]] = right + 1;
        maxLength = (right - left + 1) > maxLength ? (right - left + 1) : maxLength;
        right++;
    }
    return maxLength;
}

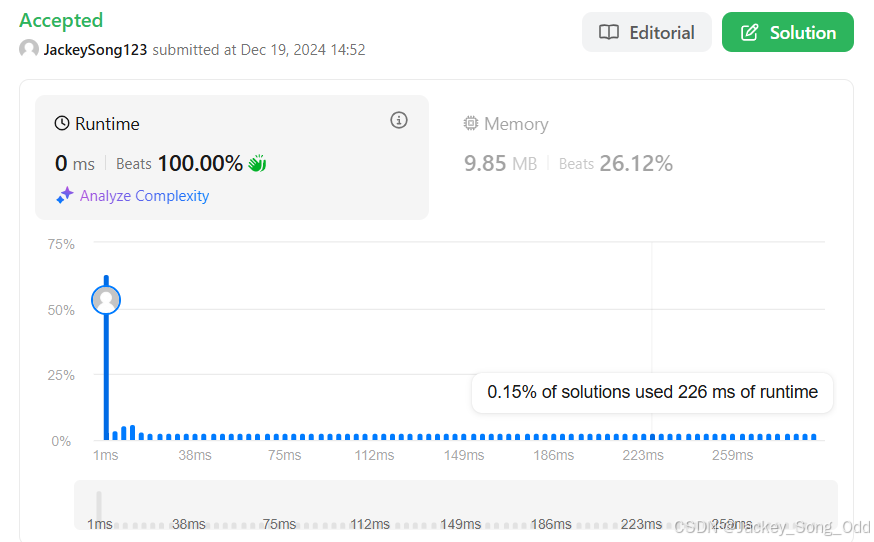
提交代码：过辣！！！打败了 100% 的人！运行时间快到了只有 0 毫秒！

在这里插入图片描述

Solution2 解释：

map 字符串数组充当一个 Hash Table 的角色，长度为 128，因为根据题意，字符串中的字符都在 ASCII 字符的范围内，0~127 。map 所有的值初始化为 0 。在这里 map 存储的是 字符（键） 和 该字符最后出现的位置（值） 的关系。

left 和 right 两个变量当作字符串位置指针，指向一个滑动窗口，窗口内没有重复字符。通过移动 right 来扩展窗口，直到窗口内没有重复字符。通过移动 left 来收缩窗口，去除重复的字符。

maxLength 最长无重复子字符串的长度。

n 字符串 s 的长度。

while 循环中不断滑动窗口，来找到最大无重复子字符串的长度。

代码加上详细注释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int lengthOfLongestSubstring(char* s) {
    int map[128] = { 0 };  // 用来记录字符的上一个出现位置
    int left = 0, right = 0, maxLength = 0;  // 初始化左指针、右指针和最大长度
    int n = strlen(s);  // 字符串的长度
    while (right < n) {  // 遍历字符串
        if (map[s[right]] > 0) {  // 如果当前字符已经在窗口内出现过
            left = (map[s[right]] > left) ? map[s[right]] : left;  // 移动左指针
            //判断当前出现的这个重复字符的上一次在字符串中的位置是否大于 left
            //大于，则重新赋值 left 为上一个重复字符的位置 + 1 处，
        }
        map[s[right]] = right + 1;  // 字符就是0~127中的一个值，将这个值当作 map 下标，更新当前字符的位置
        //因为 map 里面所有的值初始化时全部赋值为0，所以这里后面要加一个1，避免误判。
        /*
        比如，第一个字符为a, 此时下标为0，map[97] = 1;
        第二个字符为a，进入下一次循环的时候，就可以正确判断出字符a出现过了
		*/
        
        maxLength = (right - left + 1) > maxLength ? (right - left + 1) : maxLength;  // 更新最大长度
        right++;  // 右指针向右移动，这里right自增1，就是在遍历整个字符串
    }
    return maxLength;  // 返回最长子串的长度
}

Solution2 时间复杂度和空间复杂度分析

时间复杂度分析

  1. 初始化：

    1
    2
    3
    int map[128] = { 0 };
    int left = 0, right = 0, maxLength = 0;
    int n = strlen(s);
    • 初始化 map 数组需要 O(128) = O(1) 时间，因为数组的大小是固定的（128），与输入字符串的长度无关。
    • left、right、maxLength 和 n 变量的初始化都是常数时间 O(1)。

  2. 主循环：

    1
    2
    3
    4
    5
    6
    7
    8
    while (right < n) {
        if (map[s[right]] > 0) {
            left = (map[s[right]] > left) ? map[s[right]] : left;
        }
        map[s[right]] = right + 1;
        maxLength = (right - left + 1) > maxLength ? (right - left + 1) : maxLength;
        right++;
    }
    • while (right < n) 循环中的核心逻辑是通过 right 指针遍历字符串一次。每次迭代中，right 指针都会向右移动一步。
    • if (map[s[right]] > 0)：这里通过哈希表（map 数组）来检查字符是否已经出现过。查询和更新操作是常数时间 O(1)。
    • left = (map[s[right]] > left) ? map[s[right]] : left：更新 left 指针的位置也是常数时间 O(1)，因为它只进行了一次比较和赋值操作。
    • map[s[right]] = right + 1：更新字符 s[right] 在 map 数组中的位置也是常数时间 O(1)。
    • maxLength = (right - left + 1) > maxLength ? (right - left + 1) : maxLength：计算当前窗口长度并更新最大值是常数时间 O(1)。
    • right++：移动 right 指针也是常数时间 O(1)。

  3. 总结：

    • 主循环的次数是与字符串的长度 n 成正比的，因为 right 指针遍历整个字符串，每次移动一步。
    • 在每次循环中，所有的操作（包括条件判断、更新、赋值等）都需要 O(1) 时间。

因此，整个主循环的时间复杂度是 **O(n)**，其中 n 是字符串的长度。

空间复杂度分析

  1. 空间使用：

    1
    int map[128] = { 0 };
    • map 数组的大小是 128，因为假设字符集是 ASCII 字符集，最多有 128 个字符（从 0 到 127）。这个数组的大小是固定的，因此它的空间复杂度是 **O(1)**。

  2. 其他变量：

    • left、right、maxLength 和 n 等变量只占用常数空间 **O(1)**。

  3. 总结：

    • 该算法没有使用额外的动态内存分配，除了 map 数组外没有其他需要显著空间的结构。
    • 因此，空间复杂度是 **O(1)**。
Data_Structure/Algorithms_数据结构与算法
Prev:
识别有效的IP地址和掩码并进行分类统计
Next:
HTTP 版本的演进

    • Copyright © 2024 Jackey Song