前置

定义一个结构体，如下：

typedef struct node {
	int data;    //节点中的数据
	struct node *next;     //struct node 类型的指针
} Node;    //typedef 定义的别名为 Node

使用 malloc() 来为结构体申请内存，如下：

Node *head = (Node*)malloc(sizeof(Node));
head->data = 1;//为数据赋值
head->next = NULL;

我们多次使用 malloc() 函数来申请 Node 结构体大小的内存，并将所有的 Node 节点通过 next 指针连起来。这样就可以得到一个链表，由于所有的节点都指向下一个节点，所以它是单向的，这样链表被称为单向链表。head 保存了第一个节点的内存地址，通过 head 我们就可以遍历所有的 Node 节点。最后一个节点的 next 指针赋值为 NULL 作为链表的结束标志。所有节点的内存地址在内存中不一定就是连续的，它是通过指针赋值地址的方式将所有的节点连在一起的。

删除节点时，要 free(节点内存地址) 释放对应节点的内存地址，释放前要确保节点指针的断开与连接，以免造成节点丢失的问题。

---

完整单向链表示例：

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点
struct Node {
    int data;           // 节点存储的数据
    struct Node* next;  // 指向下一个节点的指针
};

// 创建新节点
struct Node* createNode(int data) {
    struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

// 在头节点前面插入新节点
void insertAtHead(struct Node** head, int data) {       //struct Node **head 二级指针，指向指针的指针，如果传入 head 一级指针，我们只能修改 head 指向的内容，而无法修改指针本身，传入二级指针可以修改 head 指针本身
	/*
	指针的本质是一个变量，变量里面保存的是一个内存地址。
	一级指针 head 保存的是链表第一个 Node 节点的内存地址。
	二级指针是 head 这个变量的内存地址，*head 赋值新创建的节点的内存地址。
	*/
    struct Node* newNode = createNode(data);
    newNode->next = *head;
    *head = newNode;
}

//在链表末尾添加节点
void insertAtTail(struct Node** head, int data) {
    struct Node* newNode = createNode(data);
    if (*head == NULL) {
        *head = newNode;
    } else {
        struct Node* temp = *head;
        while (temp->next != NULL) {
            temp = temp->next;
        }
        temp->next = newNode;
    }
}

//删除头节点
void deleteAtHead(struct Node** head) {
    if (*head == NULL) {
        printf("List is empty.\n");
        return;
    }
    struct Node* temp = *head;
    *head = (*head)->next;
    free(temp);
}

//删除指定节点
void deleteNode(struct Node** head, int data) {
    if (*head == NULL) {
        printf("List is empty.\n");
        return;
    }

    struct Node* temp = *head;
    
    // 如果要删除的是头节点
    if (temp->data == data) {
        *head = temp->next;
        free(temp);
        return;
    }

    // 查找要删除的节点
    while (temp->next != NULL && temp->next->data != data) {
        temp = temp->next;
    }

    // 如果找到要删除的节点
    if (temp->next != NULL) {
        struct Node* toDelete = temp->next;
        temp->next = temp->next->next;
        free(toDelete);
    } else {
        printf("Node with data %d not found.\n", data);
    }
}

//打印所有节点
void printList(struct Node* head) {
    if (head == NULL) {
        printf("List is empty.\n");
        return;
    }

    struct Node* temp = head;
    while (temp != NULL) {
        printf("%d -> ", temp->data);
        temp = temp->next;
    }
    printf("NULL\n");
}

//销毁链表
void destroyList(struct Node* head) {
    while (head != NULL) {
        struct Node* temp = head;
        head = head->next;
        free(temp);
    }
}

int main() {
    struct Node* head = NULL;  // 初始化空链表

    // 插入节点
    insertAtHead(&head, 10);
    insertAtHead(&head, 20);
    insertAtTail(&head, 30);
    insertAtTail(&head, 40);

    // 打印链表
    printf("Linked list: ");
    printList(head);

    // 删除节点
    deleteNode(&head, 20);  // 删除值为 20 的节点

    printf("After deleting 20: ");
    printList(head);

    deleteAtHead(&head);  // 删除头节点

    printf("After deleting head: ");
    printList(head);

    // 销毁链表
    destroyList(head);
    return 0;
}

---

---

---

反转单向链表

• 原题链接 反转链表 https://www.nowcoder.com/practice/75e878df47f24fdc9dc3e400ec6058ca?tpId=295&tqId=23286&ru=/exam/oj&qru=/ta/format-top101/question-ranking&sourceUrl=%2Fexam%2Foj%3FquestionJobId%3D10%26subTabName%3Donline_coding_page
• 难度【简单】

描述

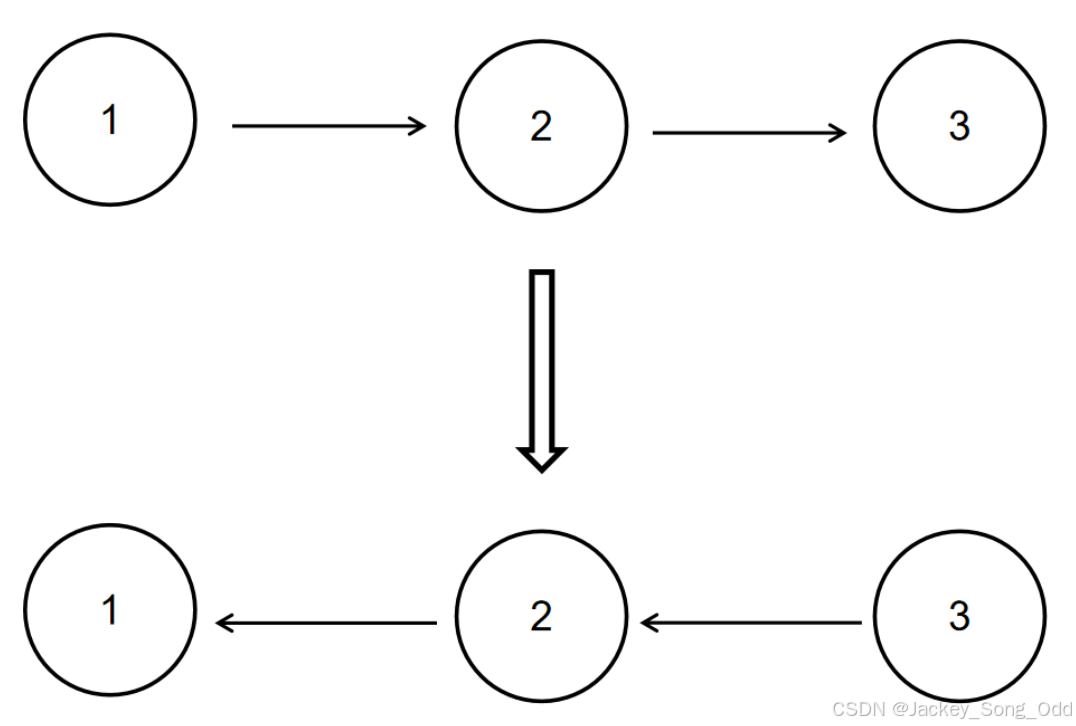
给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。

数据范围：

要求：空间复杂度 O(1) ，时间复杂度 O(n)。

如当输入链表{1,2,3}时，

经反转后，原链表变为{3,2,1}，所以对应的输出为{3,2,1}。

以上转换过程如下图所示：

示例1

输入：

{1,2,3}

返回值：

{3,2,1}

示例2

输入：

{}

返回值：

{}

说明：

空链表则输出空                 

Solution

对于单向链表的反转，关键点在在于正确处理节点的断开与连接。

而节点的断开与连接，关键点在于正确处理节点 next 指针的赋值。

在处理链表反转时，要注意不要丢失节点的指针。

代码很短很简单，但是在逻辑上要格外注意指针的赋值，以免丢失节点。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param head ListNode类 
 * @return ListNode类
 */
struct ListNode* ReverseList(struct ListNode* head ) {
    struct ListNode *pre = NULL, *cur = head, *nxt = NULL;
    while (cur) {
        nxt = cur->next;
        cur->next = pre;
        pre = cur;
        cur = nxt;
    }
    return pre;
}

时间复杂度 O(n)，一次 while 循环整个链表。

空间复杂度 O(1)。

代码解释

步骤 1：初始化

pre = NULL, cur = head (1), nxt = NULL

链表结构：

NULL <- 1 -> 2 -> 3 -> 4 -> 5 -> NULL

• nxt = cur->next，nxt = 2。
• cur->next = pre，将 1->next 指向 NULL。
• pre = cur，pre 移动到 1。
• cur = nxt，cur 移动到 2。

---

步骤 2：处理 2

pre = 1, cur = 2, nxt = NULL

链表结构：

NULL <- 1 <- 2 -> 3 -> 4 -> 5 -> NULL

• nxt = cur->next，nxt = 3。
• cur->next = pre，将 2->next 指向 1。
• pre = cur，pre 移动到 2。
• cur = nxt，cur 移动到 3。

---

步骤 3：处理 3

pre = 2, cur = 3, nxt = NULL

链表结构：

NULL <- 1 <- 2 <- 3 -> 4 -> 5 -> NULL

• nxt = cur->next，nxt = 4。
• cur->next = pre，将 3->next 指向 2。
• pre = cur，pre 移动到 3。
• cur = nxt，cur 移动到 4。

---

步骤 4：处理 4

pre = 3, cur = 4, nxt = NULL

链表结构：

NULL <- 1 <- 2 <- 3 <- 4 -> 5 -> NULL

• nxt = cur->next，nxt = 5。
• cur->next = pre，将 4->next 指向 3。
• pre = cur，pre 移动到 4。
• cur = nxt，cur 移动到 5。

---

步骤 5：处理 5

pre = 4, cur = 5, nxt = NULL

链表结构：

NULL <- 1 <- 2 <- 3 <- 4 <- 5 -> NULL

• nxt = cur->next，nxt = NULL（最后一个节点）。
• cur->next = pre，将 5->next 指向 4。
• pre = cur，pre 移动到 5。
• cur = nxt，cur 变为 NULL，退出循环。

图示

步骤	pre	cur	nxt	当前链表状态
初始	NULL	1	NULL	1 -> 2 -> 3 -> 4 -> 5 -> NULL
步骤 1	1	2	2	NULL <- 1 -> 2 -> 3 -> 4 -> 5 -> NULL
步骤 2	2	3	3	NULL <- 1 <- 2 -> 3 -> 4 -> 5 -> NULL
步骤 3	3	4	4	NULL <- 1 <- 2 <- 3 -> 4 -> 5 -> NULL
步骤 4	4	5	5	NULL <- 1 <- 2 <- 3 <- 4 -> 5 -> NULL
步骤 5	5	NULL	NULL	5 -> 4 -> 3 -> 2 -> 1 -> NULL

---

---

---

链表内指定区间反转

• 原题链接：链表内指定区间反转：https://www.nowcoder.com/practice/b58434e200a648c589ca2063f1faf58c?tpId=295&tqId=654&ru=/exam/oj&qru=/ta/format-top101/question-ranking&sourceUrl=%2Fexam%2Foj%3FquestionJobId%3D10%26subTabName%3Donline_coding_page
• 难度【中等】

描述

将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转，要求时间复杂度 O(n)，空间复杂度 O(1)。
例如：
给出的链表为 1→2→3→4→5→NULL, m=2,n=4,
返回 1→4→3→2→5→NULL.

数据范围： 链表长度 0<size≤1000，0<m≤n≤size，链表中每个节点的值满足 ∣val∣≤1000

要求：时间复杂度 O(n)) ，空间复杂度 O(n)

进阶：时间复杂度 O(n)，空间复杂度 O(1)

示例1

输入：

{1,2,3,4,5},2,4

返回值：

{1,4,3,2,5}

示例2

输入：

{5},1,1

返回值：

{5}

Solution

在 head 节点前面加上一个辅助节点，可以方便反转操作。代码有注释：

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param head ListNode类 
 * @param m int整型 
 * @param n int整型 
 * @return ListNode类
 */
struct ListNode* reverseBetween(struct ListNode* head, int m, int n ) {
    if(!head || m == n) return head;   //head为空或 m=n 则直接返回 head
    struct ListNode *start = (struct ListNode*)malloc(sizeof(struct ListNode));
    start->next = head;   //在head前面添加一个节点 start
    struct ListNode *revPre = start;   
    for (int i = 0; i < m - 1; i++)   //找到第m个节点的前一个节点 revPre
        revPre = revPre->next;
    struct ListNode *rev = revPre->next;   //rev 第m个节点
    struct ListNode *tmp = NULL;   // 临时指针
    for (int i = m; i < n; i++) {
        tmp = rev->next;   // 保存第m+1个节点的地址
        rev->next = tmp->next;      //第m个节点指向第m+2个节点
        tmp->next = revPre->next;      //第m+1个节点指向需要反转的第一个节点m
        revPre->next = tmp;      //第m节点指向第m+1节点
    }
    tmp = start->next;    // tmp 保存反转后的 head
    free(start);    //释放辅助的节点 start 的内存空间
    return tmp;    //返回 head
}

提交代码：过辣！！！